Mathematics of Dating
m |
m (→Useful links: abs stats links) |
||
| Line 28: | Line 28: | ||
== Useful links == |
== Useful links == |
||
| − | * [http://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/3201.0Jun%202007?OpenDocument Australian Population data by age] |
+ | * [http://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/3201.0Jun%202007?OpenDocument Australian Population data by age (ABS)] |
| + | * [http://www.abs.gov.au/Ausstats/abs@.nsf/7d12b0f6763c78caca257061001cc588/823B7E4F429EDB8FCA257236000117EC?opendocument Australian "MARRIAGES, DIVORCES AND DE FACTO RELATIONSHIPS" (ABS)] |
||
Revision as of 13:52, 18 February 2008
The mathematics of dating is a series of formulae of increasing comlpexity, designed to describe various variables involved in dating and romance.
Dating Pools
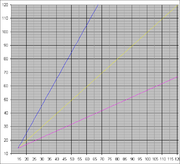
The Standard Creepiness Rule states that if we define an individual's age as x, said individual should not date anyone under:
<math>\frac{x}{2}+7</math>
By extension, this equation then also defines the maximum age an individual can date:
<math>2\,(x-7)</math>
And similarly, a combined equation will demonstrate the increasing prospective pool as one ages:
<math>2\,(x-7) - (\frac{x}{2}+7)</math>
Now, this (boring) graph shows only the ages available. However does not take into account either the population of each age bracket, nor the percentage of available partners (very simplistically: single - we will assume negligable results for gender imbalances and non-hetero partnerships for this first approximation) in each age bracket.
It has been suggested that graphing these equations will help boost your self-esteem, and generally give you something nice to put on your wall.
Failure of Dating Pool Equations to Represent User Experience
A commonly noted problem however is that environmental factors often decrease the ability of individuals to find someone with mutual interest; so that despite the fact that the estimated dating pool only increases with age, the experienced dating pool seems to be much smaller. Integral to this flaw in the equations is the shift of the 14 to 18 year highschool-oriented environment to an 18+ university/work environment, where age groups are unclearly defined, puberty has past, and mutual interests are less common.
As such there are a variety of new variables to factor into the predictive equations, and thus second-stage dating math is required.