EmojiTetra/DeepStatistics
At time of writing (Jan 2019), EmojiTetra chooses each new piece randomly with no consideration of previous pieces (there is no "bag" method). Thus there is a 1/7 chance of any given piece occurring next.
Thus, the chance of a run of, say, 5 I's is 1 in (1/7)^5, or 1 in 16807. The chance of a run of 8 I's would be 1 in 5.764801 million!
These both happened in game 15 (both runs of "I")
- Run of 8: https://twitter.com/EmojiTetra/status/1058796612418363392
- Run of 5: https://twitter.com/EmojiTetra/status/1077177730540625920
leading to this analysis...
However, that is not the chance of that happening in general, only the chance of that specific piece happening at that time. If we don't care WHICH piece is involved in the run, then it's not about a run of "8 pieces which are I", but in fact a run of "7 pieces which are the same as the piece before it". That's 1 in 823542.
But what about the truly general question of "what is the chance of it happening at all, at any time, in a game of (say) length 1811 pieces (ie, game15, in which we had both the run of 5 and run of 8)
For that, it gets... complex...
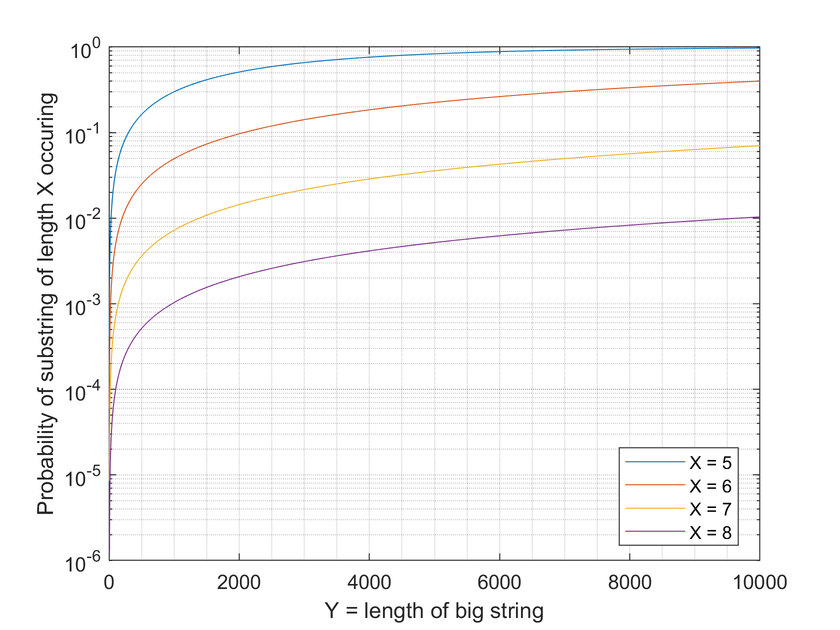
Graph showing probability of a substring of length X (for X=5,6,7,8) being identical characters in a big string length Y, where Y is populated from only 7 possible characters. Note that in Game 15, Y (length of game by count of pieces) was 1811, and as of 3rd January 2018, all games give us Y=4427
For a more detailed writeup, the prepared analysis was given to me in RTF format and I've not wiki'ised it.
In game 25, we got a
And subsequent analysis (linked to middle of thread, with graphs) https://twitter.com/skrymir42/status/1129866971741396992